Introduction To Artificial Neural Network
03 Mar 2017Artificial Intelligence (AI) သို့မဟုတ် မြန်မာဘာသာစကားဖြင့် “တုပဖန်တီးထားသော ဥာဏ်ပညာ” “ဥာဏ်တု”ဟု အဓိပွါယ်ဖွင့်ဆိုနိုင်သည့် ကွန်ပျူတာ သိပွံပညာရပ်ခွဲတစ်ခုသည် ယခု ကျွနု်ပ်တို့ နေ့စဥ်လှုပ်ရှားသွားလာနေထိုင်နေသော IT ခေတ်ကြီးတွင် တနေ့ထက်တနေ့ အလွန်အရေးပါလှသော အခန်းကဏ္ဍမှ သိသိသာသာ နေရာယူလာသည့်အလျောက် မရှိမဖြစ်လိုအပ်လာသည်။ AI စနစ်တို့ဖြင့် လူသားတိုင်း အမှုမဲ့ အမှတ်မဲ့ ထိတွေ့နေရသော ကာလဖြစ်သည်။ Apple၏ iOS အသုံးပြုသူများသည် Siri ဟုခေါ်သော AI စနစ် တစ်ခုဖြင့် အသားကျနေသကဲ့သို့ Google၏ Android device အသုံးပြုသူများသည်လည်း Google Now ဟုခေါ်သော AI စနစ်ဖြင့် အကျွမ်းတဝင်ရှိနေပြီးဖြစ်သည်။ ၄င်း AI စနစ်တို့ကြောင့် လူသားတို့၏ နေ့စဥ်လူနေမှုဘဝ သက်တောင့်သက်သာဖြင့် ပိုမိုအဆင်ပြေချောမွေ့လာစေသည်။ မိမိ သိလိုသည်များကို smart device များတွင် တိုက်ရိုက် ရိုက်သွင်းစရာ မလိုတော့ဘဲ နှုတ်ဖြင့် မေးမြန်းရုံဖြင့် စက္ကန့်ပိုင်း အတွင်း သင့်တော်ဆီလေျာ်မှန်ကန်စွာ ဖြေကြားပေးနိုင်သည်။ အဘယ်ကြောင့်ဆိုသော် ယင်း AI စနစ်တို့သည် လူသားအချင်းချင်း ဆက်သွယ်ရာတွင် အသုံးပြုသော ဘာသာစကားတို့ကို လူကဲ့သို့ မြင်ရုံ၊ ကြားရုံဖြင့် နားလည်နှိုင်စွမ်းရှိခြင်းဖြစ်သည်ဟုပင် ဆိုရပေမည်။ ဤကဲ့သို့ ကွန်ပျူတာတစ်လုံးအား စဥ်းစားတွေးခေါ်တတ်စေရန် သင်ကြားပေးသည့် အတတ်ပညာကို တနည်းအားဖြင့် Machine Learningဟုလည်းဆိုပေသည်။ အလားတူပင် အင်တာနက်မှ စျေးဝယ်ရာတွင်လည်း မိမိ ကြိုက်နှစ်သက်ဖွယ်ရှိသည့် ကုန်ပစ္စည်းများကို စျေးဝယ်သူ တစ်ဦးချင်းစီ၏ အကြိုက်ကိုလိုက်၍ အလိုအလျောက် recommendation/suggestion များအနေဖြင့် ကြေငြာပေးသည့် စနစ်များသည်လည်း AI agent များပင်ဖြစ်သည်။ မိုးလေဝသခန့်မှန်းချက်များ တွက်ချက်ရာမှာ အစ၊ Facebook တွင် မိမိနှင့် သိကျွမ်းရင်းနှီးဖွယ်ထင်ရလောက်သည့် မိတ်ဆွေများကို အလိုအလျောက် Friend suggestion အနေဖြင့် အကြံပြုပေးသည့်စနစ်အဆုံး AI agents များပင်ဖြစ်သည်။ AI ၏ အဓိကရည်ရွယ်ချက်မှာ မေးခွန်း/ပုစ္ဆာ/ပြသနာတစ်ခုကို နားလည်သဘောပေါက်၍ ယင်းပြသနာနှင့် ဆီလျော်မှန်ကန်သော အဖြေ/တုံ့ပြန်မှုတစ်ခုကို အနီးစပ်ဆုံး မှန်မှန်ကန်ကန် ပြန်လည်ဖြေကြားပေးနိုင်စေရန်ဖြစ်သည်။ ဤသည်မှာ လူသားတို့ နေ့စဥ်ထိတွေ့နေရသော တုပဖန်တီးပြုလုပ်ထားသော Artificial Intelligence ဟုခေါ်သော ပညာရပ်တစ်ခု၏ အကျဥ်းဖြစ်သည်။
Neural Network ၏ နိယာမ
ယနေ့ စာရေးသူမှ ၄င်းAIစနစ် သို့မဟုတ် လူသားတစ်ယောက်ကဲ့သို့ တွေးခေါ်တတ်စေရန် ကွန်ပျူတာအား သင်ကြားရာတွင် အသုံးပြုလေ့ရှိသော စနစ်များထဲမှ တစ်ခုဖြစ်သည့် Artificial Neural Network(ANN) ဟုဆိုသော စနစ်တစ်ခုကို အလွယ်ကူဆုံး ရှင်းလင်းသွားမည်ဖြစ်သည်။ ANN သည် လူသားတို့၏ ဦးနှောက်အတွင်း Neurons များ တခုနှင့် တခု ချိတ်ဆက် သတင်းပို့ ဆက်သွယ်မှုကို အတုယူ ဖန်တီးထားခြင်းသာဖြစ်သည်။ လူ့ဦးနှောက် အလုပ်လုပ်ပုံကို အခြေခံပြီး ကွန်ပျူတာများအား လူကဲ့သို့ စဥ်းစားတွေးခေါ်တတ်စေရန် သင်ကြားပို့ချပေးသောစနစ်တစ်ခုဖြစ်သည်။ Neural Network တစ်ခုတွင် neurons များနှင့် ၄င်းတို့အချင်းချင်း ဆက်သွယ်ပေးသော synapses များ ပါဝင်သည်။ Neuron တစ်ခုသည် ၄င်း၏ dendritesများမှ input signal ကို လက်ခံရရှိ၍ output signal ကို ၄င်း၏ axon မှတဆင့် ထုတ်လုပ်ပေးသည်။ ယင်းaxonမှတဖန် ခွဲဖြာဖြန့်ကျက်၍ တခြား neuron ၏ dendrite သို့ synapseမှတဆင့် ဆက်သွယ်ကူးလျှက်ခြင်းဖြင့် neuron တခုနှင့်တခု ဆက်သွယ်လုပ်ဆောင်ကြသည်။ ဦးနှောက်တွင်းရှိ neuron တစ်ခု၏ လုပ်ဆောင်ပုံမှာ အောက်ဖော်ပြပါ ပုံ(၁)အတိုင်းဖြစ်သည်။
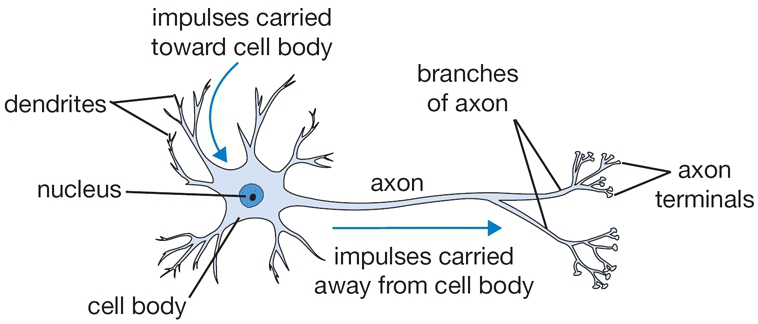
ပုံ(၁) ဦးနှောက်တွင်းရှိ Neuron တစ်လုံး၏ လုပ်ဆောင်ပုံ
ပုံ(၂)တွင်ကား ဦးနှောက်တွင်းရှိ neuronများ အချင်းချင်း ချိတ်ဆတ် အလုပ်လုပ်ပုံကို တုပတီထွင်ထားသော Neural Network ၏ ဝိသေသဖြစ်သည်။ ဤဝိသေသ၏ ဖြစ်တည်မှုသဘောတရားနှင့် လုပ်ဆောင်ချက်များကို တဆင့်ချင်း ရှင်းပြသွားမည်ဖြစ်သည်။
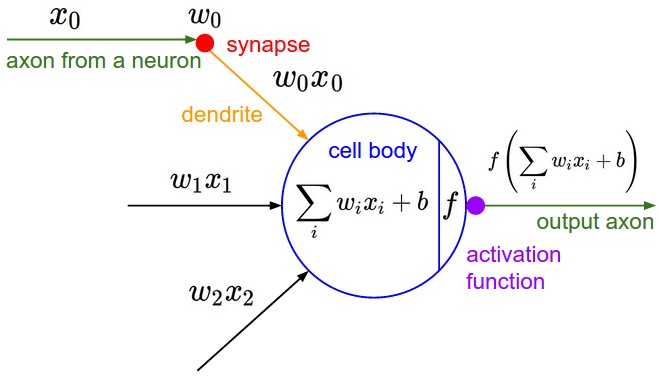
ပုံ(၂) Neural Network ၏ ဝိသေသ
Neural Network တစ်ခုတွင် Input Layer, Hidden Layer နှင့် Output Layer ဆို၍ အလွှာ ၃လွှာဖြင့် ဖွဲ့စည်းတည်ဆောက်ထားသည်။ Input layer သည်ကား မေးခွန်း/ပုစ္ဆာတစ်ခုအတွက် ဖြေကြားရန် လိုအပ်သော အချက်အလက်တချို့ကို လက်ခံရရှိသည့် အလွှာဖြစ်သည်။ ဥပမာအားဖြင့်ဆိုသော် ကျောင်းသားတစ်ယောက်၏ စာကြည့်ချိန်နှင့် အိပ်ချိန်ပေါ်မူတည်၍ နောက်တနေ့ စာမေးပွဲဖြေဆိုရာတွင် ရရှိနိုင်မည့် အမှတ်စာရင်းကို တွက်ချက်ရန် ထိုကျောင်းသား၏ စာကြည့်ချိန်နှင့် အိပ်ချိန် နှစ်ခုသည် အမှတ်စာရင်းအား ခန့်မှန်းရာတွင် လိုအပ်သော အချက်အလက်ဖြစ်သည်။ ထို့ကြောင့် ကျောင်းသား၏ စာကြည့်ချိန်နှင့် အိပ်ချိန်ကို Input layer တွင် ထည့်သွင်းရမည်။ Hidden Layer ဆိုသည်ကား Input layer နှင့် Output layer ကြားတွင် ရှိပြီး ယင်းတို့ရဲ့ လုပ်ဆောင်ချက်များသည် အဓိက အချက်ချာကျသော်လည်း ထိန်ချန်ကွယ်မြှပ်ထားသောကြောင့် hidden (ကွယ်မြုပ်နေသော) အလွှာဟု ခေါ်ဝေါ်ထားခြင်းဖြစ်သည်။ Hidden layer ၏ လုပ်ဆောင်ချက်မှာ Input layer နှင့် Output layer တို့အကြား ဆက်နွယ်မှုကို လိုက်လျောညီထွေစွာ တွက်ချက် အဖြေဖော်ထုတ်ပေးခြင်းဖြစ်သည်။ ယင်းလုပ်ဆောင်ချက်များကို အသေးစိတ်ရှင်းလင်းပေးသွားပါမည်။ နောက်ဆုံး အလွှာဖြစ်သည့် Output layer ဆိုသည်မှာ Input layer ၏ အချက်အလက်များနှင့် အကိုက်ညီဆုံးသော အဖြေကို ဖြေဆိုပေးခြင်းဖြစ်သည်။ Neural network တစ်ခုတွင် Input layer, hidden layer, output layer ပါရှိသောကြောင့် အလွှာ ၃လွှာသာရှိသည်ဟု ယူဆ၍မရပါ။ အလွန့်အလွန် ခက်ခဲရှုပ်ထွေးလှသော အခြေအနေမျိုးတို့တွင် Hidden layerသည် အလွှာ ၁လွှာထက်မနည်း ရှိတတ်သည်။
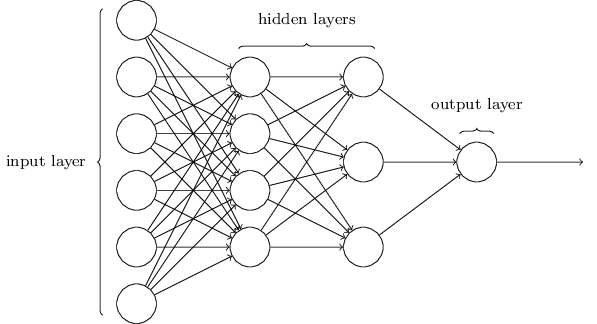
ပုံ(၃) Artificial Neural Network ၏ တည်ဆောက်ပုံ သာဓက
ပုံ(၃)တွင် မြင်တွေ့ရသည့်အတိုင်း Input layer ၁လွှာ၊ Hidden layer ၂လွှာနှင့် Output layer ၁လွှာ စုစုပေါင်း အလွှာ ၄လွှာဖြင့် neural network တစ်ခု ဖွဲ့စည်းတည်ဆောက်ထားသည်ကို တွေ့ရမည်ဖြစ်သည်။ Input layerရှိ စက်ဝိုင်းများသည် neurons များကို ကိုယ်စားပြုသောကြောင့် ၄င်း input layerတွင် neuron ၆လုံးပါရှိသည်။ ထိုနည်းလည်းကောင်း ပထမ hidden layer တွင် neuron ၄လုံး၊ ဒုတိယ hidden layer တွင် neuron ၃လံုးနှင့် output layer တွင် neuron ၁လုံးပါရှိသည်။ Input layer, hidden layer နှင့် output layer တို့တွင် neuron ဘယ်နှစ်လုံးပါရှိရမည်ဟု ကန့်သတ်ထားခြင်းမျိုး မရှိပေ။ မိမိအဖြေရှာလိုသည့် ပုစ္ဆာသဘောတရားပေါ် မူတည်၍ ပြောင်းလဲ သတ်မှတ်နိုင်သည်။ Input layer ရှိ neuron များနှင့် hidden layer ရှိ neuron များ ဆက်သွယ်ထားသည့် မြှားတန်းများသည် ဦးနှောက်တွင်းရှိ dendrite များ အဖြစ် သတ်မှတ်နိုင်ပြီး ၄င်းမြှားတန်းများတွင်လည်း ကိုယ်ပိုင် ဂုဏ်သတ္တိ ကိန်းဂဏန်းများ (weight) တည်ရှိနေသည်။ ထို့ကြောင့် အလွှာတစ်ခုနှင့် တစ်ခုကြား ချိတ်ဆက်ရာတွင် neuron တခု၏ ဂုဏ်သတ္တိ နှင့် weight တို့ ပေါင်းစပ်ခြင်းဖြင့် တခြားသော neuron တခု၏ ဂုဏ်သတ္တိကို ဖြစ်ပေါ်စေသည်။ ဤသို့ဖြင့် output layerရှိ neuron များ ဖြစ်တည်သည်အထိ တွက်ချက်သွားခြင်းဖြစ်သည်။
Training & Testing in Machine Learning
Neural Network ၏ လုပ်ဆောင်ပုံကို အသေးစိတ် မရှင်းလင်းခင် ပထမရှေးဦးစွာ Machine Learning ၏ Training နှင့် Testing သဘောသဘာဝကို ရှင်းလင်းသွားပါမည်။ ထို့ကြောင့် Training နှင့် Testing ၏ သဘောသဘာဝကို နားလည်ထားပြီးဖြစ်သူများသည် ဤစာပိုဒ်အား ချန်လှပ်ထားနိုင်သည်။
Artificial Intelligence သို့မဟုတ် Machine Learning သည် ကွန်ပျူတာများအား စဥ်းစားတွေးတော၍ မှန်ကန်ဆီလျော်သော တန့်ပြန်ချက်များဖြေကြားပေးနိုင်စေရန် သင်ကြားပေးရသော ဘာသာရပ်တစ်ခုဖြစ်သည်။ ဤကဲ့သို့ သင်ကြားပေးရာတွင် Training နှင့် Testing ဆို၍ အပိုင်း ၂ပိုင်း ပါရှိသည်။
Training ဆိုသည်မှာ ပုစ္ဆာနှင့် တကွ အဖြေပူးတွဲ ပါရှိပြီးသော ဒေတာများဖြင့် ညွှန်ပြပေးခြင်းဖြစ်သည်။ Input နှင့် Output result ကို ဖော်ပြထားပြီး ကွန်ပျူတာအား input ရဲ့ အခြေအနေပေါ် မူတည်၍ ၄င်း၏ output အဖြေမှန်ကို မှတ်သားထားစေပြီးလျှင် ယင်း training data များ၏ hypothesis တခုကို learning algorithms များ အသုံးပြု၍ ရှာဖွေစေသည်။ ၄င်းလုပ်ငန်းစဥ်ကို Training ဟုခေါ်ဆိုခြင်းဖြစ်သည်။ အလွယ်ကူဆုံးသော သာဓကပေးရလှျင် အသက်(၂)နှစ်မှ(၈)နှစ်အတွင်းရှိ ကလေးသူငယ်တို့၏ အသက်အရွယ်အလိုက် ပျမ်းမျှ အရပ်အမြင့်ကို ရှာမည်ဆိုပါစို့။ စစ်တမ်းကောက်ချက်များအရ အောက်ဖော်ပြပါဇယား(၁)အတိုင်း dataset တစ်ခု ရရှိမည်ဖြစ်သည်။
| age(x) | height(y) |
|---|---|
| 2 | 0.7 |
| 2 | 0.5 |
| 3 | 0.9 |
| 5 | 1.1 |
| 4 | 1 |
| … | … |
ဇယား(၁) - ကလေးသူငယ်တို့၏ အသက်ရွယ်အလိုက် အရပ်အမြင့်ပြ စစ်တမ်း
ယင်း dataset အား x,y two-dimensional plot တစ်ခုတွင် ချကြည့်မည်ဆိုလျှင် ပုံ(၄)အတိုင်းရရှိမည်ဖြစ်သည်။
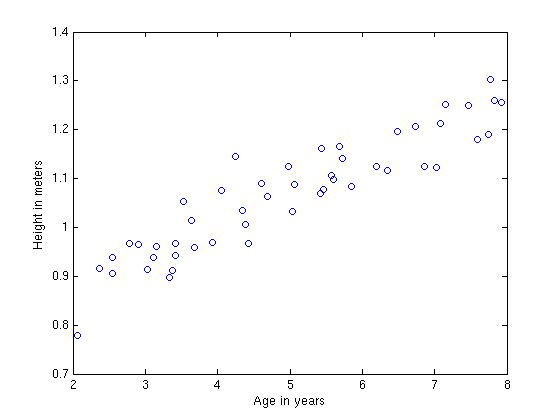
ပုံ(၄) ကလေးသူငယ်တို့၏ အသက်အရွယ်အလိုက် အရပ်အတိုင်းအတာပြ ဇယား
Hypothesis ဆိုသည်မှာ x နှင့် y ကိန်းတို့၏ ဆက်နွယ်မှုကို ရှာဖွေခြင်းဖြစ်သည်။ input နှင့် output data တို့၏ ဆက်နွယ်မှုကို ပီပြင်ပေါ်လွင်စေရန် အဖြေရှာခြင်းဖြစ်သည်။ အထက်ပါ ရရှိသော data plot တွင် hypothesis မျဥ်းရှာဖွေရာတွင် အလွယ်ကူဆုံးအနေနဲ့ Linear regression ဟုခေါ်သော algorithm ကို အသုံးပြု၍ ရှာလျှင် ပုံ(၅)အတိုင်း data plot အရ hypothesis မျဥ်း ရေးဆွဲနိုင်မည်ဖြစ်သည်။ ၄င်းမျဥ်းရှာဖွေခြင်းကို ယခုဥပမာတွင် training process ဟုခေါ်နိုင်ပေသည်။
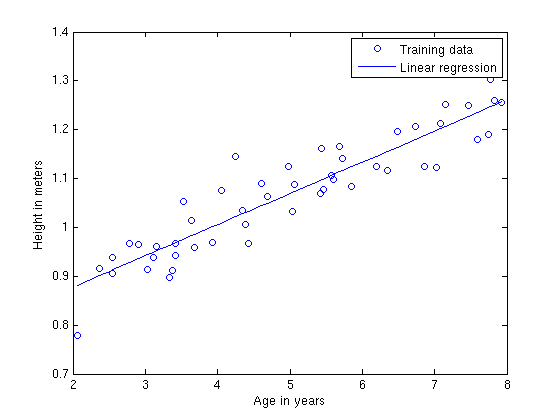
ပုံ(၅) ကလေးသူငယ်တို့၏ အသက်အရွယ်အလိုက် အရပ်အတိုင်းအတာပြ ဇယား
ထို့နောက် ရရှိသော hypothesis (အဆိုကြမ်း)အား Test data သို့မဟုတ် ပုစ္ဆာ/မေးခွန်း (input data) သာပါ၍ အဖြေ(output)မပါသော ဒေတာများတွင် အစားထိုး၍ အဖြေခန့်မှန်းရယူခြင်းဖြစ်သည်။ x သည် input data ဖြစ်၍ ၄င်းကိန်းအား ရှာဖွေရရှိထားသော hypothesis တွင် အစားထိုးခြင်းဖြင့် y ကိန်းကို ရရှိမည်ဖြစ်သည်။ ၄င်းကို Testing ဟု ခေါ်ဆိုသည်။
Training a Neural Network
Neural network တစ်ခုအား လေ့ကျင့်သင်ကြားစေခြင်း သို့မဟုတ် train ရသည့် အဓိက ရည်ရွယ်ချက်မှာ neural network အတွင်းရှိ weight ဂုဏ်သတ္တိများကို ညှိနှိုင်းဖော်ထုတ်စေခြင်းဖြစ်သည်။ ဤကဲ့သို့ လေ့ကျင့်သင်ကြားရာတွင် အေရးပါဆုုံးသော လုပ်ဆောင်ချက် ၂မျိုး ပါဝင်နေပြန်သည်။ ၄င်းတို့မှာ
Forward propagation - Neural network အတွင်း input data များအား Random weight များဖြင့် ရှေးဦးစွာ ပေါင်းစပ်တွက်ချက်၍ output data ရှာဖွေခြင်းဖြစ်သည်။ Network ၏ရှေ့မှနောက်သို့ ကျပန်း weight များကို အသုံးပြု၍ တွက်ချက်သွားခြင်းဖြစ်သည်။
Back propagation - Forward propagation တွင် ရှေ့မှနောက်သို့ input data ကနေတဆင့် ကျပန်း weight များ အသုံးပြု၍ ရရှိသော output data နှင့် မူရင်းအဖြေမှန် output data တို့အား ပြန်လည်စိစစ်၍ အဖြေနှစ်ခု၏ ကွာခြားချက်(Margin of error)ကို နည်းသထက်နည်းအောင် နောက်မှေရှ့သို့ error margin အနည်းဆုံးဖြစ်စေမည့် weight များကို ပြန်လည်ဖော်ထုတ်ခြင်းဖြစ်သည်။
အထက်ပါ လုပ်ဆောင်ပုံအဆင့်ဆင့်ကို သာဓကနှင့်တကွ ဆက်လက်ရှင်းလင်းသွားမည်ဖြစ်သည်။ အလွယ်ကူဆုံးသော သာဓကအနေဖြင့် Logic gate များမှ XOR gate ၏ လုပ်ဆောင်ပုံအား Neural network အသုံးပြု၍ အဖြေထုတ်ပုံကို ဥပမာပေးရှင်းလင်းသွားမည်ဖြစ်သည်။ XOR gate ၏ ဂုဏ်သတ္တိအား ဇယား(၂)အတိုင်း တွေ့နိုင်သည်။
| Input | Output |
|---|---|
| 0 xor 0 | 0 |
| 0 xor 1 | 1 |
| 1 xor 0 | 1 |
| 1 xor 1 | 0 |
ဇယား(၂) - XOR gate ၏ ဂုဏ်သတ္တိပြဇယား
Forward propagation
XOR gate ၏ ဂုဏ်သတ္တိသည် ဇယား(၂)တွင် တွေ့ရှိရသည့်အတိုင်း Input data နှစ်ခုပါရှိ၍ Output data တစ်ခုတည်းသာဖြစ်သည်။ ဥပမာအနေဖြင့် XOR gate ၏ ၄ဆင့်မြောက် ဂုဏ်သတ္တိအား Neural network တွင် ထည့်သွင်း၍ Training process လုပ်ဆောင်စေရန် forward propagation network အတွင်း Input data နှစ်ခုနှင့် output data အား ထည့်သွင်းမည်ဆိုလှျင် ပုံ(၆)အတိုင်း တွေ့မည်ရမည်ဖြစ်သည်။
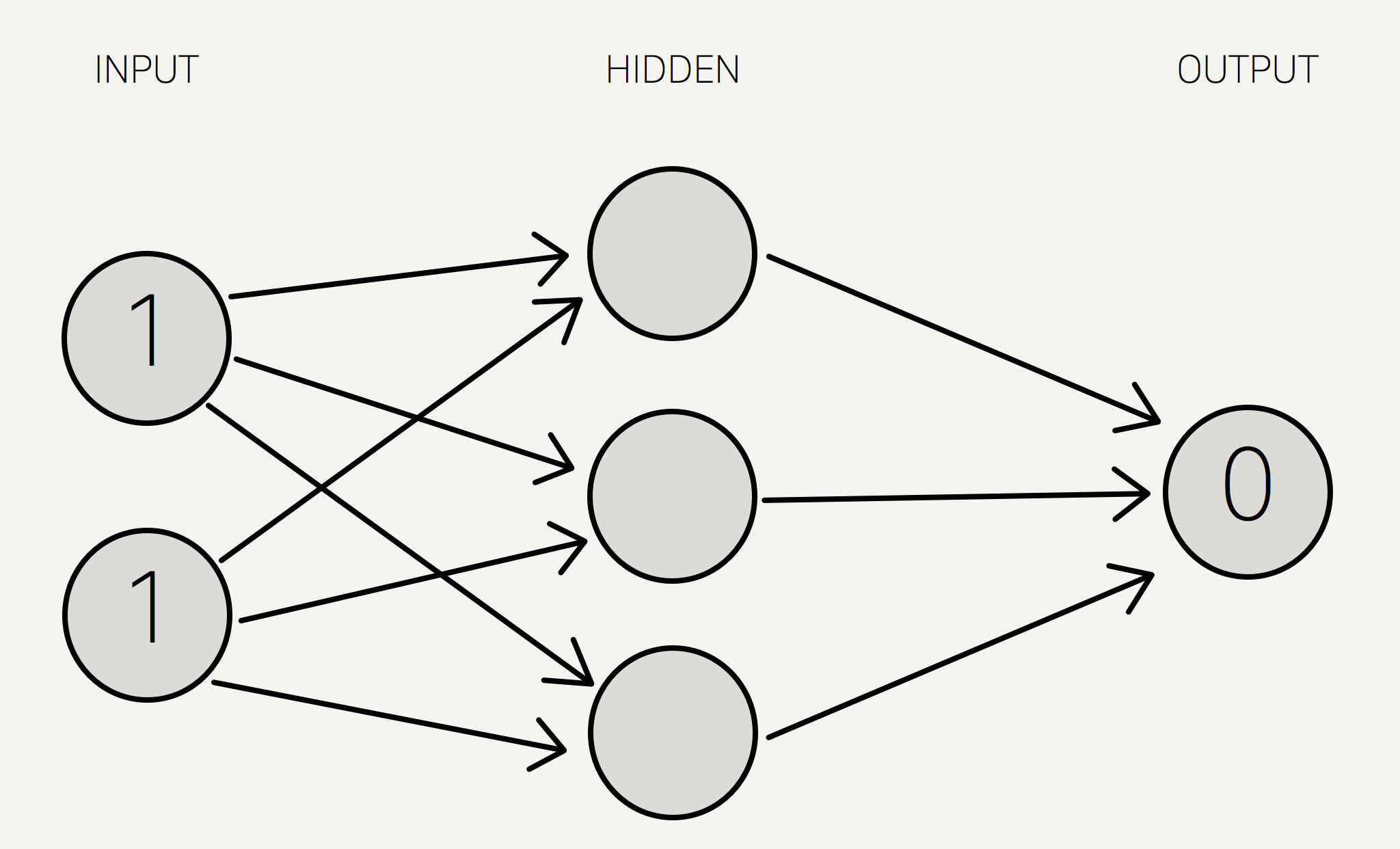
ပုံ(၆) XOR gate ၏ ဂုဏ်သတ္တိ (1, 1,) => 0 အား Neural network အတွင်း ထည့်သွင်းခြင်း
ထို့နောက် network အတွင်းရှိ neuron တစ်ခုနှင့် တစ်ခု ချိတ်ဆက်ထားသော မြှားတန်းများ(synapse)ကို ကျပန်း weight များအနေဖြင့် ၀ မှ ၁ အတွင်းရှိ ကိန်းဂဏန်းများအား ပုံ(၇)အတိုင်း ရှေးဦးစွာ သတ်မှတ်ရမည်ဖြစ်သည်။
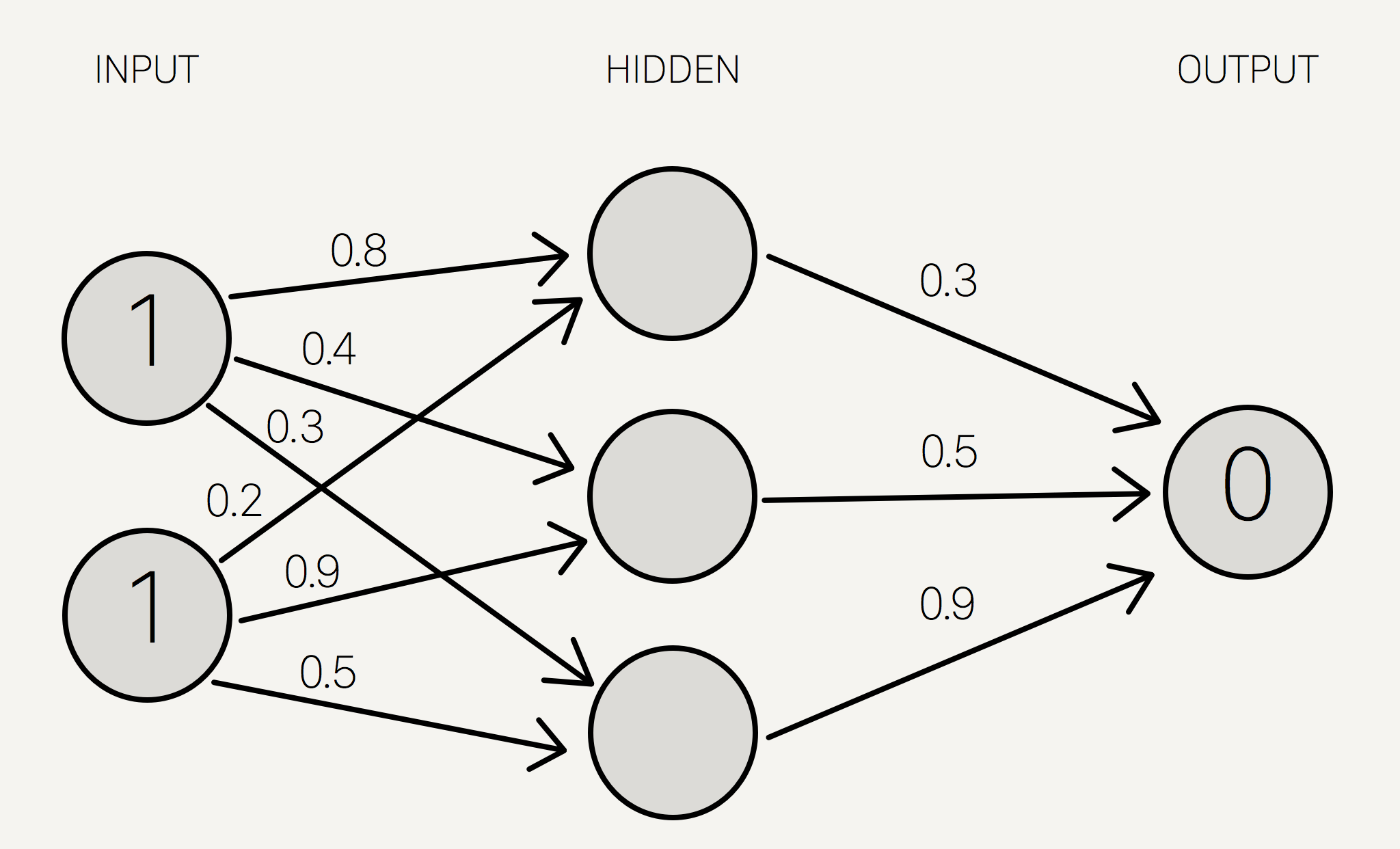
ပုံ(၇) Neural network အတွင်းရှိ synapse များအား ကျပန်း weight များ သတ်မှတ်ခြင်း
ကျပန်း weight များ သတ်မှတ်ပြီးနောက် Input layer အတွင်းရှိ neuron များနှင့် synapse များ၏ weight များအား convolution နည်းအရ အဆင့်ဆင့် တွက်ချက်သွားလျှင် Hidden layer အတွင်းရှိ neuron ၃လုုံး၏ ဂုဏ်သတ္တိများ ရရှိမည်ဖြစ်သည်။
\[y_j = \sum_{i}x_i w_{j,i}\]
အထက်ဖော်ပြပါ ပုံသေနည်းတွင် \(x_i\)သည် \(i\) အလုံးမြောက် input neuron ဖြစ်၍ \(y_j\)သည် \(j\) အလံုးမြောက် hidden layerအတွင်းရှိ neuronဖြစ်သည်။ \(w_{j,i}\)သည်ကား \(i\) အလုံးမြောက် input layer၏ \(j\) အလုံးမြောက် synapse ဖြစ်သည်။
\[y_0 = x_0 w_{0,0}+ x_1 w_{0,1} = (1 * 0.8) + (1 * 0.2 )= 1\] \[y_1 = x_0 w_{1,0}+ x_1 w_{1,1} = (1 * 0.4) + (1 * 0.9 )= 1.3\] \[y_2 = x_0 w_{2,0}+ x_1 w_{2,1} =(1 * 0.3) + (1 * 0.5 )= 0.8\]သို့သော် ၄င်း ကိန်းဂဏန်းများသည် hidden layer အတွင်း neuron များ၏ စင်စစ်ဂုဏ်သတ္တိများ မဟုတ်သေးသဖြင့် ခေတ္တ/ယာယီ ကိန်းဂဏန်းများ အနေဖြင့် ပုံ(၈)အတိုင်း သတ်မှတ်ထားနိုင်သည်။
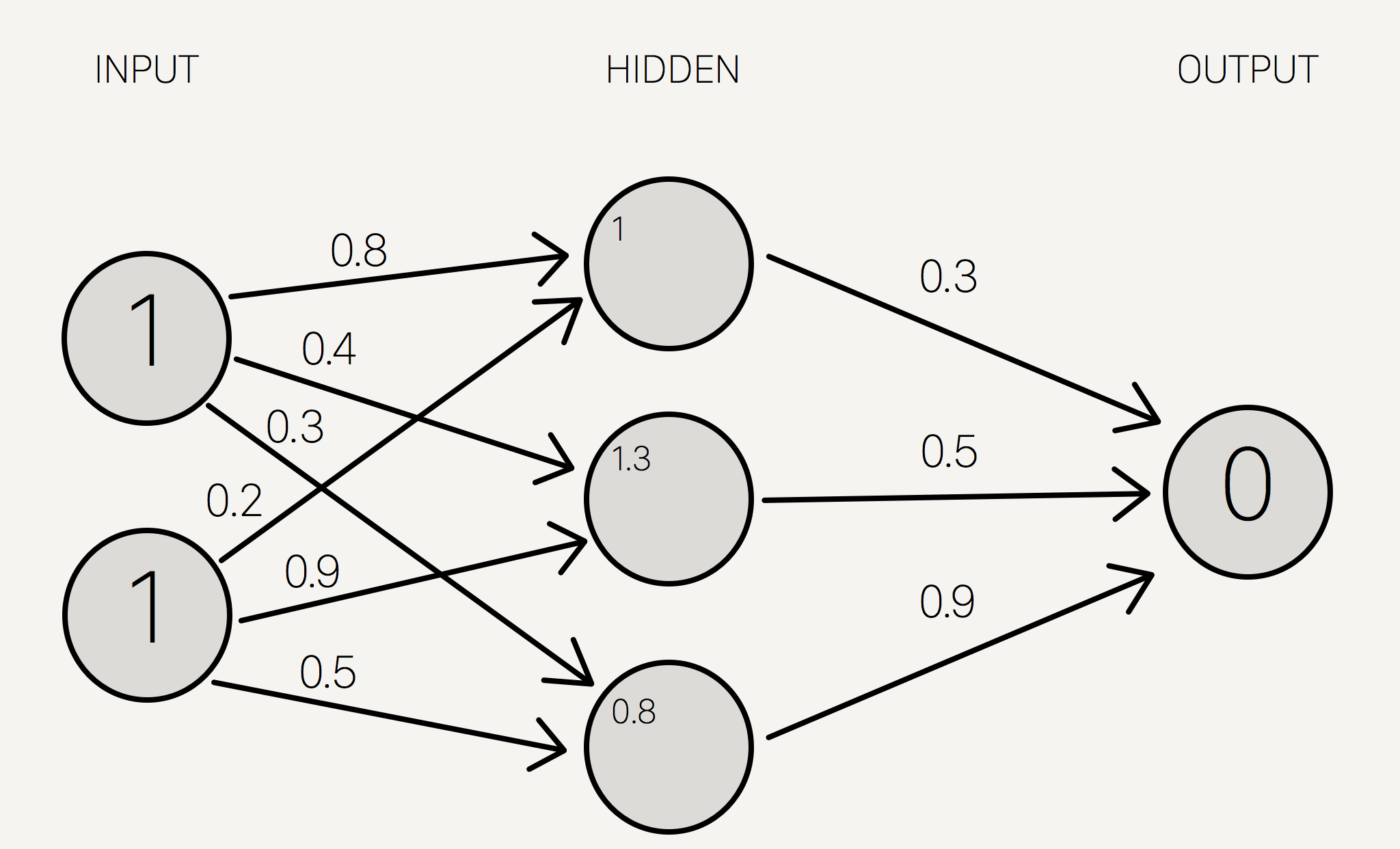
ပုံ(၈) Hidden layerအတွင်းရှိ neuron များ၏ ယာယီ ကိန်းဂဏန်းများ တွက်ချက်ပုံ အဆင့်ဆင့်
ထို့နောက် ရရှိပြီးသော ကိန်းဂဏန်းများအား hidden layerအတွင်းရှိ neuron တို့၏ စင်စစ်ဂုဏ်သတ္တိ ကိန်းဂဏန်းအဖြစ် သတ်မှတ်စေနိုင်ရန် ဆက်လက် တွက်ချက်သွားရမည်ဖြစ်သည်။ ယင်းဖြစ်စဥ်ကို Activation function ဟုလည်း ခေါ်ဝေါ်အသုံးပြုကြသည်။ ထိုသို့ ရရှိလာသော ကိန်းဂဏန်းများသည်လည်း ၀ မှ ၁ အတွင်း၌သာရှိစေရန် အလို့ငှာ Linear regression, logistic regression (Sigmoid), hyperbolic tangent နှင့် အခြားသော function များထဲမှ တစ်ခုကို အသုံးပြုနိုင်မည်ဖြစ်သည်။ Activation function ၏ အဓိက ရည်ရွယ်ချက်သည် network အတွင်းရှိ neuron တို့၏ ဂုဏ်သတ္တိများကို linear သဘောအရ ရှုပ်ထွေးနက်နဲစွာ အဖြေရှာခြင်းထက် non-linear သဘောတရားအရ ကိန်းဂဏန်းများအား ကျစ်ကျစ်လစ်လစ် အတိုချုံး၍ အဖြေထုတ်နိုင်ရန်၊ ဆုံးဖြတ်ချက် အလွယ်တကူ သုံးသပ်နိုင်ရန်ဖြစ်သည်။ ဥပမာအားဖြင့်ဆိုသော် \(၀.၅\) နှင့် \(၁\) အထက် ကိန်းဂဏန်းများရှိလျှင် ၄င်းတို့အား \(၁\) ဟု သတ်မှတ်၍ \(၀.၅\) အောက် လျော့ကျသော ကိန်းများအား \(၀\) ဟုသာ သတ်မှတ်နိုင်ရန်ဖြစ်သည်။ ထိုသို့သတ်မှတ်ရာတွင်ပုံ(၉)တွင် ဖော်ပြထားသည့် functionများအနက် သင့်တော်ရာ တစ်ခုအား အသုံးပြုနိုင်သည်။
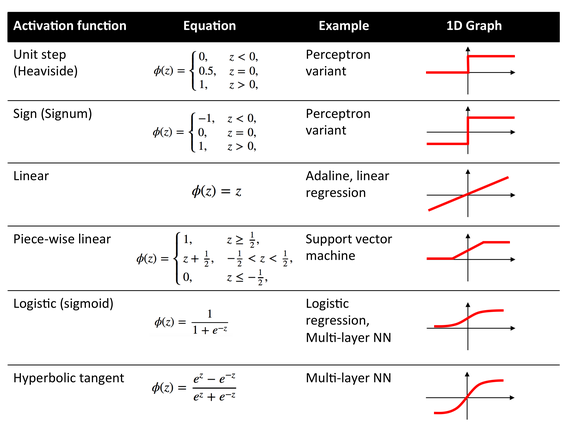
ပုံ(၉) Activation functions []
ယခု သာဓကအနေနှင့် Activation function အတွက် sigmoid function ကိုသာ အသုံးပြုသွားမည်ဖြစ်သည်။ ထို့ကြောင့် ရရှိထားပြီးဖြစ်သော ယာယီကိန်းများအား activation function ပုံသေနည်းဖြင့် အစားသွင်း အဖြေထုတ်လျှင် အောက်ပါအတိုင်းရရှိမည်ဖြစ်သည်။
\[S_0(1.0) = 0.731\] \[S_1 (1.3) = 0.785\] \[S_2 (0.8) = 0.689\]ထို့ကြောင့် Hidden layer ၏ neuron များကို သက်ဆိုင်ရာ ဂုဏ်သတ္တိကိန်းများဖြင့် သတ်မှတ်နိုင်ပြီဖြစ်သည်။
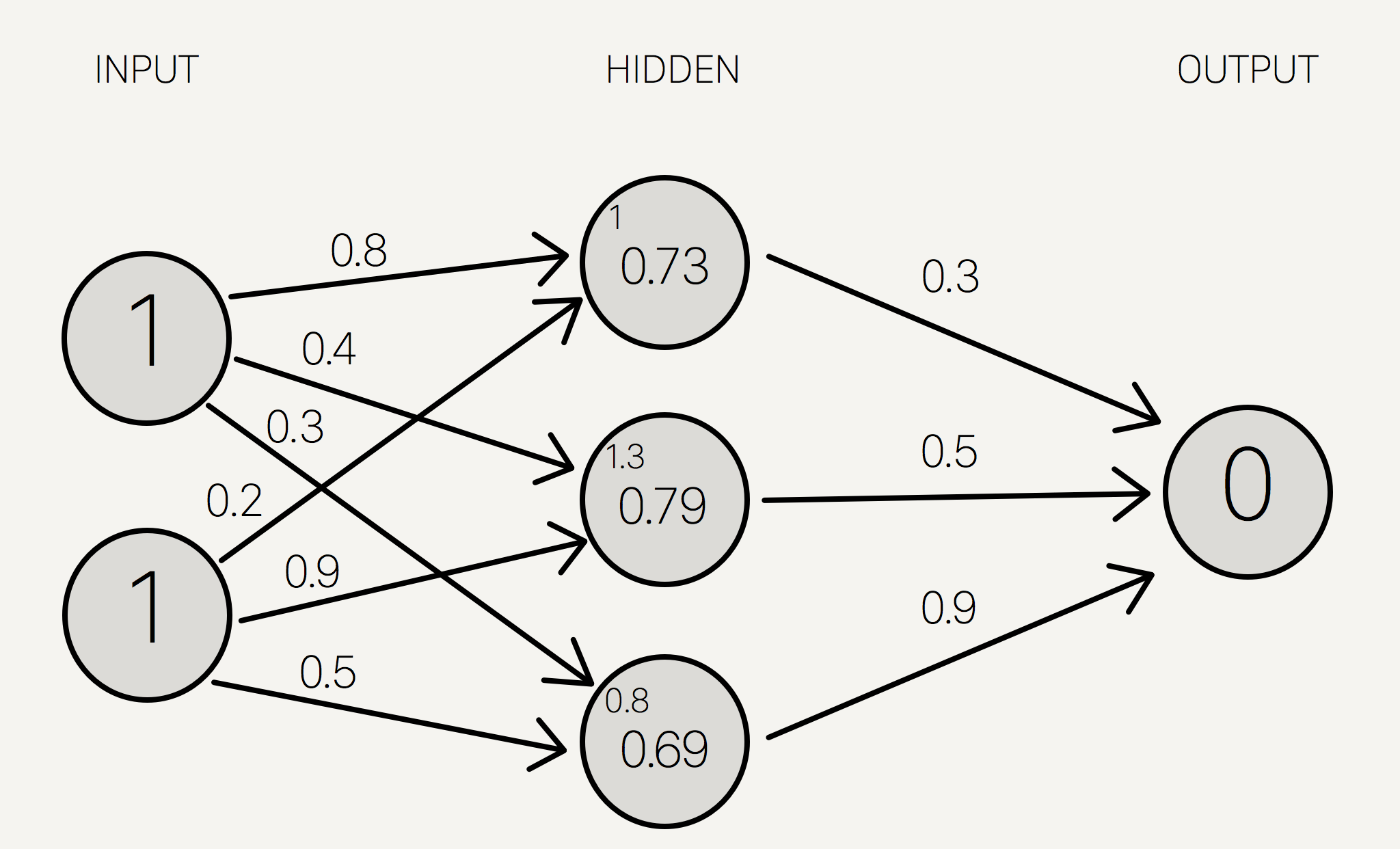
ထို့နောက်တဖန် convolution နည်းအရ ပြန်လည်တွက်ချက်ခြင်းဖြင့် Output layer၏ neuron တန်ဖိုးကို ရရှိနိုင်မည်ဖြစ်သည်။
\[O = 0.73 * 0.3 + 0.79 * 0.5 + 0.69 * 0.9 = 1.235\]ရရှိလာသည့် အဖြေအား ထပ်မံ၍ activation function ဖြင့် အစားထိုးတွက်ချက်လျှင် neural network ၏ output prediction ကို ပုံ(၁၁)အတိုင်း တွေ့ရှိရမည်ဖြစ်သည်။
\[S_o (1.235) = 0.774\]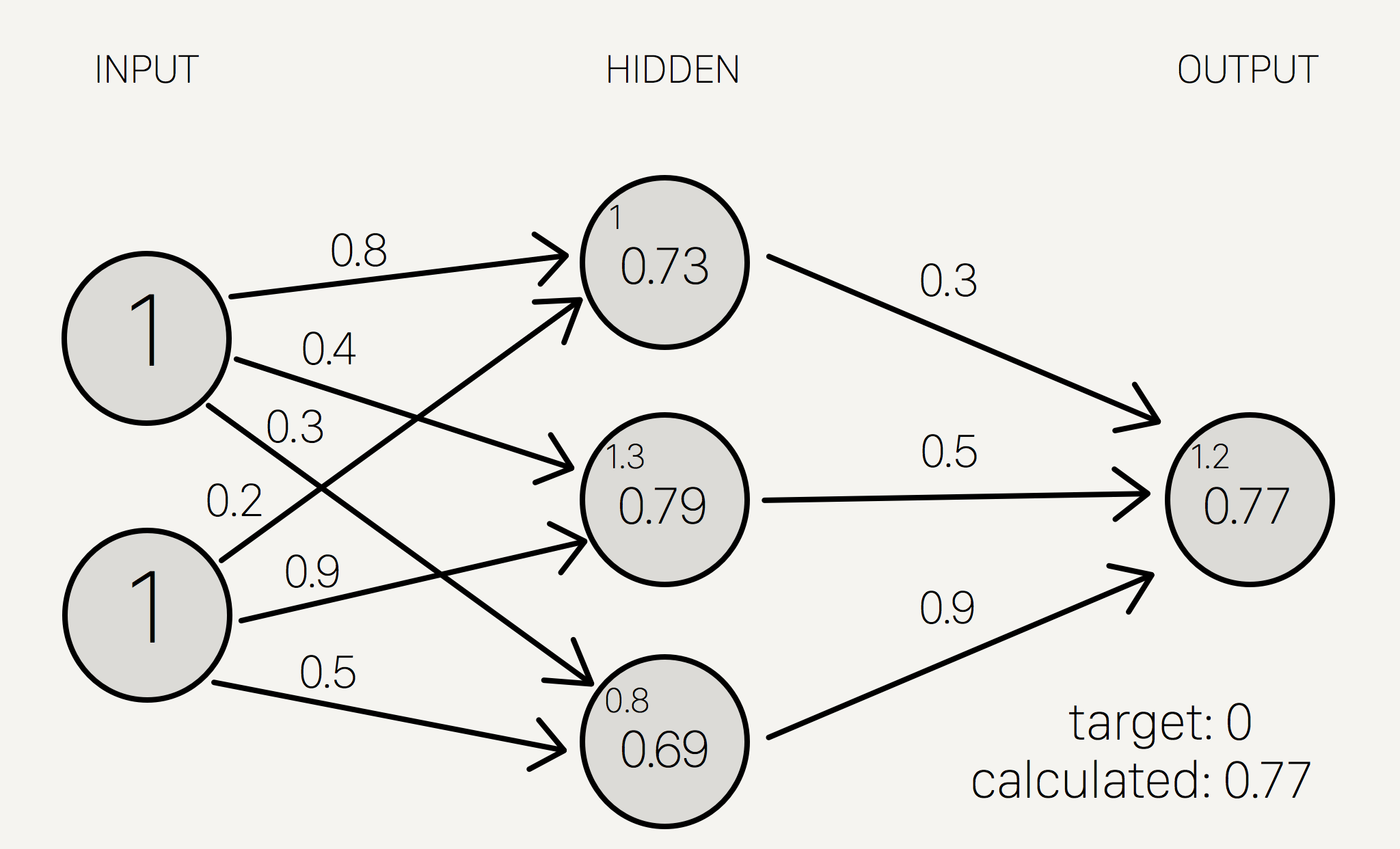
အထက်ပါပုံတွင် တွေ့ရသည့်အတိုင်း weight များသည် ကျပန်းေရွးခြယ်ထားခြင်းဖြစ်သောကြောင့် output အဖြေသည် ဆီေလျာ်မှန်ကန်စွာ ထွက်ဆိုနိုင်မည်မဟုတ်ပေ။ Neural network အား ယခုလက်ရှိအနေထားတွင် ရပ်တန့်ထားလိုက်မည်ဆိုပါက မှန်ကန်သော XOR gate ၏ ဂုဏ်သတ္တိကို တွက်ချက်နိုင်မည် မဟုတ်ပေ။ ထို့ကြောင့် အဖြေမှန်အား ထုတ်ဖော်ရရှိနိုင်ရန် back propagation နည်းလမ်းအား အသုံးပြု၍ ဆက်လက်ရှာဖွေသွားရန် လိုအပ်ပေသည်။
Back propagation